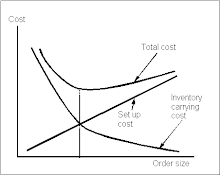
In the paper "EOQ and EPQ with linear and fixed backorder costs: Two cases identified and models analyzed without calculus" by Sphicas, the author extends algebraic analysis to EOQ and EPQ with both linear and fixed backorder costs without using any skill of calculus. Moreover, this paper provides further insights into the EOQ and EPQ models with additional obervations.
The author states the conditions to determine whether backorders are too expensive or backorders should be carried by comparing the per unit operational cost without backorders and the total fixed cost of backordering everything. The size of the linear backorder cost doesn't affect the optimal choice.
A correction to previous works is that even if the value of 2KD(h+p) - (pai)^2 D^2 is positive, it may not achieve the optimal Q. The exact range for (pai)D was reported.
The eventual optimal total cost is the same as it would be if the maximum inventory was continuously carried and nothing else happened.
Another special case is identified that if only one backorder cost is assumed, both Q and S are infinite when considerring backorders. The author provides an eaiser proof of this known result than using calculus.
The algebraic analysis of EPQ model is basically similar.
- Bing Liu
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment